"O sábio lê livros, e lê também a vida. O universo é um grande livro e a vida é uma grande escola."
as coincidências que desafiam o acaso
por Hans Manfred Heuer
O psicólogo suíço Carl Gustav Jung (1875-1961) e o físico laureado com o prêmio Nobel Wolfgang Pauli (1900-1958) introduziram na psicologia o conceito de “sincronicidade” para ocorrências de acontecimentos acausais simultâneos, ligados por um sentido comum, tanto na natureza como na psique (acasos inevitáveis, fenômenos psi, etc.).
Quem nunca ouviu falar do acúmulo casual de acontecimentos importantes, muitas vezes dramáticos em certas datas, ou em determinado ano para muitas famílias ? Não é como se o destino às vezes “insistisse em escolher” determinados lugares e datas para acontecimentos semelhantes? É o caso dos exemplos que se seguem:
“Na semana passada, nas proximidades de Fürstenwalde, um motociclista foi apanhado pela locomotiva de um trem e arrastado para a morte. Há seis anos, a mãe da vítima perdeu a vida da mesma forma e quase no mesmo local. Como revelou a pesquisa, tratava-se da mesma locomotiva e do mesmo condutor, sem que este tivesse a menor culpa disso.” -
Trata-se de uma antiga notícia de jornal, cuja data não pode mais ser precisada - basta ler o jornal com atenção para encontrar, quase que diariamente, notícias semelhantes.
Seguem alguns casos especialmente marcantes:
“O destino, muitas vezes, segue caminhos estranhos. Assim ele determinou que dois moradores de Fautenbach em Achern-in-Baden (seus pais eram irmãos e eles também eram vizinhos) não só fossem internados no hospital no mesmo dia, como também que ambos morressem no mesmo dia e fossem levados para sua última morada sexta-feira passada.” (Do Badische Neueste Nachrichten de 10/4/1972. )
“Estranhos casos de morte assolaram na semana passada uma família de Ichenheim, distrito de Lahr. Com 61 anos de idade, Emma Nautascher faleceu depois de breve enfermidade. Sua irmã Maria, com quem viveu por muitos anos, seguiu-a, três dias depois, com 77 anos. E quase na mesma hora morria a terceira irmã Anna Blasi, nascida Nautascher, com 64 anos, no hospital, vítima de derrame cerebral.” (Do Acher-und Büh- ler Bote de 11/7/1972.)
Tragicamente interessante em todos esses casos é a relação familiar, que muitas vezes desempenha um papel, como mostra o caso seguinte:
“Na mesma semana os irmãos da rainha Sílvia da Suécia foram seriamente acidentados. Ambos, Jorg Sommerlath, de 36 anos, e Ralf Sommerlath, de 48, tiveram um acidente automobilístico em lugares distintos...” (Bild, l/12/1977.)
O médico dr. Wilhelm Fliess (1858-1928) - que defende em sua (amplamente discutível) “teoria dos períodos” a opinião de que “as ondas periódicas, que atravessam nosso corpo, determinando sua vida e bem-estar, doença e morte, não dizem respeito apenas ao indivíduo isolado, mas atravessam ao mesmo tempo toda a geração que tem o mesmo sangue . . .” - esclarece com suas descobertas, entretanto, apenas uma parte das estranhas “duplicidades” determinadas pela consangüinidade, como as que se manifestam nos exemplos citados, justamente as coincidências de casos de doença e morte na mesma família. Esses exemplos, no entanto, também estão submetidos àquela força de atração misteriosa, quase mágica, que se encontra nos casos de “duplicidade” ou sincronicidade, cuja atuação é muito mais ampla, já que não se limita à consangüinidade.
Mesmo assim, queremos acrescentar aqui mais um exemplo, que se encaixa na “teoria dos períodos”, por se tratar de algo bastante raro. Na primavera de 1960, a revista Schweizer Illustrierte publicou a foto de uma “família bissexto”, acompanhada do seguinte texto:
“A cegonha da família sueca Berggren, de Charlottenberg, tem tido o capricho de por três gerações aparecer pontualmente no dia 29 de fevereiro. O avô Goran Berggren, seu filho Gosta e a esposa deste, Britta, nasceram todos num dia bissexto, e agora sua filhinha também nasceu no dia 29 de fevereiro deste ano. Os Berggren desafiam qualquer família da Europa a bater seu recorde - o que, sem dúvida, é bastante difícil.”
Wilhem von Scholz descreve um exemplo oposto: “O médico L. Th. (de Württemberg) atendeu em 1924 dois casos de extraordinária coincidência. Casos duplos de doença ou morte já eram há muito conhecidos na clínica, mas dessa vez o jogo do destino foi mais longe. Duas crianças foram a seu consultório. Ambas chamadas Helmut Haller, os dois pais chamados Wilhelm Haller, ambas nascidas em junho de 1921, ambas com a mesma moléstia (bronquite), ambas internadas ao mesmo tempo, os dois pais trabalhando no mesmo setor. As duas crianças eram loiras, de olhos azuis e de temperamento bem incomum.
“As famílias eram provenientes de regiões distintas, não tinham nenhum parentesco e não se conheciam até o momento (pelo menos as mães). Os pais só ouviram falar um do outro no local de trabalho.
“Um funcionário de confiança visitou as duas famílias, residentes em Z., em lugares opostos. Seu relatório:
“Helmut Haller, rua B número 72, em Z., nascido a 8 de junho de 1921. Não há ninguém mais na família com o nome de Helmut.
“Helmut Haller, rua A número 115, em Z., nascido a 27 de Junho de 1921. Não há mais ninguém na família com o nome de Helmut.
“Em Z. existem sete médicos. Os meninos Helmut Haller devem ser as únicas pessoas da Terra que nasceram no mesmo mês do mesmo ano e cujos pais se chamam Wilhelm Haller. E exatamente esse ‘par’ veio parar em Z., proveniente de lugares distintos, sem que as duas famílias jamais se tivessem conhecido, vindo a ser tratado no mesmo mês pelo mesmo médico, da mesma doença, enquanto os pais se empregavam na mesma oficina.
“A semelhança no preenchimento das fichas dos doentes onde são anotados nome e sobrenome, ano e mês de nascimento das crianças, nome e sobrenome do pai, doença e seguro de doença (também o mesmo) e data de tratamento - levou o médico a acreditar que preenchera duas vezes a mesma ficha. Da mesma forma, o caixa desculpava-se por um suposto erro cometido.”
Embora esses casos devam ser vistos como raridades, estou convencido de que uma pesquisa sistemática e intensiva nesse domínio traria à luz outras raridades, pois a natureza se compraz com tais “extravagâncias’, como se quisesse nos mostrar do que é capaz, deixando-nos às voltas com enigmas.
Mesmo que alguns casos de “duplicidade” se encontrem separados no tempo, devem ser vistos nesse contexto, como o demonstram os exemplos seguintes, que têm apenas uma coisa em comum: a “predileção” do destino por um nome especial . . .
No dia 5 de dezembro de 1664, o navio inglês “Menay” naufragou em Pas de Calais em meio a uma tempestade. Dos 81 passageiros salvou-se apenas um, um certo Hug Williams.
No dia 5 de dezembro de 1785, uma escuna foi atirada por um temporal às costas da ilha Man. Sessenta pessoas estavam a bordo e todas se afogaram, com exceção de uma. O sobrevivente se chamava Hug Williams.
A 5 de agosto de 1820 um vapor de passageiro chocou-se com um rebocador no rio Tamisa. Vinte e cinco passageiros, em sua maioria crianças por volta de 12 anos, perderam a vida nesse acidente. Apenas o pequeno Hug Williams, que embarcara em Londres para visitar Liverpool, foi levado para terra com vida.
A 19 de agosto de 1889, um cargueiro de carvão sofreu um naufrágio. Sua triputação de nove homens encontrou a morte. Apenas dois, tio e sobrinho, ambos de nome Hug Williams, sobreviveram, sendo salvos por pescadores.
Casos de duplicidade, sincronicidade - simultaneidade de acontecimentos com pessoas e lugares e em relação com nomes, números e datas -, podem ser acrescentados aqui à vontade. Cada um de nós já se defrontou alguma vez com experiências desse tipo, seja pessoalmente ou por intermédio de pessoas da família, amigos ou vizinhos. Como sobre todos os fenômenos ainda não bem esclarecidos, são muitas as opiniões a respeito da “duplicidade de acontecimentos” da simultaneidade de fatos semelhantes.
O materialista dirá que não passam de disposições fortuitas de acontecimentos, de “caprichos do destino”. O crente irá aceitá-las como vontade de Deus, o cientista irá vê-las no contexto das leis de causa e efeito, o filósofo, de acordo com sua visão de mundo.
Uma coisa parece certa: em fatos humanos atua um certo magnetismo. Existe uma força de atração que produz tudo aquilo que chamamos “acaso” (inclusive sob forma de duplicidade de acontecimentos). Entretanto, essa força de atração, como podemos observar em casos raros, não é naturalmente a única força motora de nossa existência humana, embora atue misteriosamente em toda parte. Ela é algo “acrescentado “ .
Vamos partir do princípio de que existem forcas que se delineiam claramente diante da razão, que atuam de forma conseqüente e que não têm nada de misterioso em si. Essa chamada força de atração, contudo, se esquiva a qualquer cálculo e controle da vontade; pelo contrário, é prejudicada pela consciência, pois se oculta da razão, não parece atuar de forma, conseqüente, mas surge de forma repentina e imprevista de uma relação de início invisível. Ela aparece como algo estranho, que vem de fora. Nisso se encontra sua relação com o destino. Também o destino, na acepção lata do termo, é algo estranho e que vem de fora. É aquilo que , independente da marcha desejada e prevista das coisas, irrompe do exterior, exigindo, ou muitas vezes impedindo, de forma decisiva.
Em seu texto sobre “A Aparente Intencionalidade no Destino do Indivíduo”, o filósofo alemão Arthur Schopenhauer (1788-1860) afirma que tudo é duvidoso, não só a solução como até mesmo o problema. Segundo ele, trata-se de andar tateando no escuro, onde se percebe que há alguma coisa, sem que se possa saber bem o que nem onde. Mas em seguida ele postula, em uma observação filosófico-metafisica, uma necessidade rígida, pela qual tudo que acontece é produto de uma cadeia causal coesa, e menciona os videntes e profetas como “prova empírica” de que em cada momento existente estão contidos em germe todos os momentos futuros do mundo com todos os seus milhões de particularidades.
Se se quer denominar o destino de unidade última de acaso e necessidade íntima, é preciso supor que as vítimas da “duplicidade de acontecimentos” - para o bem ou para o mal - conjuraram elas mesmas os incidentes, justamente pela “necessidade íntima”.
Segundo Schopenhauer, “casual” significa o encontro no tempo do que não se liga por causalidade. A essa tese Wilhelm vou Scholz opõe o seguinte: “Nada é absolutamente casual; o mais fortuito é apenas algo necessário que percorreu um caminho mais distante, pois uma causa decisiva situada num ponto remoto da cadeia causal há muito já determinou que ocorresse exatamente agora e com isso ao mesmo tempo que aquilo outro. Cada acontecimento é um elo isolado da corrente de causa e efeito que progride na direção do tempo. Mas existem infinitas correntes dessas paralelas no espaço. Entretanto, elas não são totalmente estranhas e sem vínculos entre si; ao contrário, se entrelaçam de muitas maneiras: por exemplo, muitas causas que atuam nesse momento, produzindo cada uma efeitos diferentes, surgiram de uma mesma causa remota, e por isso são aparentadas como os bisnetos de um bisavô; por outro lado, um único efeito que surge agora exige muitas vezes o concurso de muitas causas distintas, que vêm do passado como elos de suas próprias correntes.
“Por conseguinte”, segue Scholz, “todas as correntes causais que progridem na direção do tempo formam uma grande rede comum entrelaçada, que em toda sua extensão avança no sentido do tempo, constituindo o andar do mundo. Imaginemos agora essas cadeias causais isoladas como meridianos situados no sentido do tempo: a simultaneidade não pode ser indicada na mesma linha causal, e sim por círculos paralelos. Embora fatos situados sob o mesmo círculo não dependam imediatamente um do outro, o entrelaçamento de toda a rede, ou o conjunto de causas e efeitos que avança no sentido do tempo, faz com que tais fatos tenham algum tipo de ligação, ainda que longínqua, e portanto sua simultaneidade é necessária. Aqui, o encontro casual de todas as condições se aproxima de um acontecimento necessário no mais alto sentido: o acontecer daquilo que o destino quis.
Assim, em última conseqüência todos os casos de “duplicidade” ou “sincronicidade” não são de modo algum simples acasos ou brincadeiras da natureza, como muitas vezes somos levados a acreditar, e sim acontecimentos que desde o princípio aguardam seu desempenho, o qual só ocorre quando é dada esta ou aquela condição.
Sem dúvida, resta saber se algum dia conseguiremos captar as relações profundas desses fenômenos, de forma que seja possível, partindo de “hipóteses de trabalho” ou “modelos de pensamento”, chegar a um conhecimento Claro da regularidade e da previsibilidade dos acontecimentos do destino.
Fonte: Grupo de Estudos Cinturão de Fotons - Texto extraído da Revista Planeta Número 156, Setembro de 1985
.
.
" Você esta aqui para possibilitar que o propósito divino do universo se revele.Veja como você é importante! "Eckhart Tolle
Arrisque... o risco é a unica maneira de você saber se está "realmente" Vivo!!!
Zoia Petrow
.
sincronicidade
a repressão cria o inconsciente.
"Não estou aqui para convencê-los sobre coisa alguma. Não estou aqui para lhes dar um dogma, uma crença para viver. Estou aqui para tirar todas as crenças de vocês porque somente assim a vida acontecerá a vocês. Não estou dando algo para que vocês vivam através disso, estou simplesmente tirando todas as escoras de vocês, todas as muletas."
Exponha-se...Osho“... Se você conseguir expor-se religiosamente, não na privacidade, não com seu psicanalista, mas simplesmente em todos os seus relacionamentos... Isto é autopsicanálise. Isso é vinte quatro horas de psicanálise, todos os dias. Isso é psicanálise em todo tipo de situação: com a esposa, com o amigo, com os parentes, com o inimigo, com o estranho, com o chefe, com o seu funcionário. Por vinte e quatro horas você está se relacionando.
Se você continuar se expondo... No começo vai ser realmente muito assustador, mas logo você começará a ganhar força porque uma vez que a verdade é exposta, ela se torna mais forte e a não verdade morre. E com a verdade tornando-se mais forte, você se tornará mais enraizado e centrado. Você começa a se tornar um indivíduo. A personalidade desaparece e o indivíduo aparece.
A personalidade é falsa e a individualidade é substancial. A personalidade é simplesmente uma fachada e a individualidade é a sua verdade. A personalidade lhe é imposta de fora, é uma persona, uma máscara. A individualidade é a sua realidade, ela é como Deus a fez. A personalidade é uma sofisticação social, um polimento social. A individualidade é crua, selvagem, forte e com tremendo poder.
... Uma vez que você esteja pronto, corajoso e desafiador; uma vez que você tenha experimentado a liberdade da verdade, a liberdade de expor a sua realidade, você poderá seguir por si mesmo. Você conseguirá ser uma luz para si mesmo.
Mas o medo é natural porque desde o início da infância, lhe foram ensinadas falsidades, e você se tornou tão identificado com o falso que abandoná-lo quase parece cometer suicídio. E o medo surge porque uma grande crise de identidade aparece.
... O medo é natural. Não o condene e não sinta que ele é algo errado. Ele é apenas parte de toda essa educação social. Nós temos que aceitá-lo e ir além dele. Sem condená-lo, nós temos que ir além dele.
Exponha pouco a pouco, não há qualquer necessidade de você dar saltos que você não possa administrar. Vá passo a passo, gradualmente. Mas logo você irá descobrir o sabor da verdade.
... A repressão cria o inconsciente. Quanto mais reprimido você for, maior o inconsciente que você tem. O que na verdade é o inconsciente? Ele é aquela parte de sua mente que fica de lado, é aquela parte de sua casa onde você nunca vai, o porão. Você vai atirando ali todo tipo de coisas e nunca você vai lá. (...)
O inconsciente é uma criação da civilização. Quanto mais civilizado você for, mais inconsciente você será. Se você for absolutamente civilizado, você será um robô, você será absolutamente inconsciente. Isso é o que está acontecendo. Esta calamidade está acontecendo em todo o mundo. Isso tem que parar. E a única maneira de parar isso é ajudando as pessoas a colocar para fora os seus inconscientes nas meditações. Exponha-se. Isso será um alívio...”
(OSHO - The Guest)
hiperdimensionalidade parte - II -
4D - Quarta Dimensão
texto e imagens: Dr. Bernardo de Gregório
revisão, atualização, pesquisas, textos e imagens complementares: Zoia Petrow
Fonte: Grupo de estudos Cinturão de Fótons 2004
Na Europa no fim do Século XIX falar sobre a quarta dimensão era tema restrito a determinados círculos sociais. Eventualmente a idéia da quarta dimensão cruzou o Atlântico e veio aos Estados Unidos. O introdutor principal de todas as idéias quadridimensionais foi um matemático inglês nomeado Charles Hinton. Hinton gastou sua vida obcecado pela noção de popularizar e de visualizar a quarta dimensão. Em 1885, foi preso por bigamia na Inglaterra, por três dias. Logo em seguida, viajou para o Japão, eventualmente terminando nos E. U. em 1893.
Hinton quis criar nomes para as direções e sentidos da quarta dimensão, assim como existem na terceira:
‘para frente” e ‘para trás’
‘esquerda’ e ‘direita’
‘para cima’ e ‘para baixo’
As palavras correspondentes para a quarta dimensão eram “Ana” e “Kata”. Desta forma, se você fosse no sentido do ana na quarta dimensão então você estava indo no sentido oposto de alguém que fosse no sentido do kata.
Hinton foi também a pessoa que pensou o nome para o hipercubo quadridimensional. Chamou-o de “Tesseract”. Este hipercubo é a generalização do cubo tridimensional. Todos seus lados devem ter o mesmo comprimento.
O estudo dos politopos é um ótimo exercício para ampliar nossa visão 4D. Vamos agora utilizar as analogias para prever o número de vértices, arestas,
faces e células do hipercubo (4D) e apresentar algumas fórmulas matemáticas para calcular o número de elementos dos politopos ortogonais, que são os análogos do cubo na escada das dimensões.9.1
A figura 9.1 mostra como é simples encontrar o número de vértices de qualquer politopo ortogonal. Já vimos que o ponto, o segmento (de reta) e o quadrado são os análogos do cubo nos degraus inferiores da escada. Vamos começar com o "cubo" 0D (zero dimensão), que é o ponto. Ele tem somente 1 vértice. Quando ele é deslocado na primeira direção (para a direita), cria o "cubo" 1D (segmento), que tem 2 vértices. Quando o "cubo" 1D é deslocado na segunda direção (para trás), cria o "cubo" 2D (quadrado), que tem 4 vértices. Quando o "cubo" 2D é deslocado na terceira direção (para cima), cria o cubo 3D (o nosso cubo comum), que tem 8 vértices. Assim, seguindo a lógica, quando o cubo for deslocado na quarta direção, ele criará o hipercubo ("cubo" 4D), que é um politopo de 16 vértices.
Você deve ter notado, pela seqüência acima, que nós dobramos o número de vértices a cada degrau que subimos na escada dimensional, porque cada vértice deslocado cria mais um vértice ao final do percurso. Como regra geral, se o número de dimensões de um politopo ortogonal for n, seu número de vértices será 2n.
Vamos agora pensar sobre o número de arestas. No lado esquerdo da figura 9.2, partimos de um "cubo" 1D (segmento), que tem 1 aresta e 2 vértices. Quando ele é deslocado para trás, sua única aresta (verde) cria uma nova aresta (vermelha) ao final do percurso. Porém, cada um de seus 2 vértices gera uma nova aresta (roxa) quando se desloca. O resultado é o "cubo 2D" (quadrado), que tem 4 arestas e 4 vértices.9.2
Vamos partir agora do "cubo" 2D (quadrado), no lado direito da figura 9.2. Quando ele é deslocado para cima, suas 4 arestas (verdes) criam mais 4 arestas (vermelhas) ao final do percurso. Porém, cada um de seus 4 vértices gera uma nova aresta (roxa) quando se desloca. O resultado é o cubo comum (3D), que tem 12 arestas e 8 vértices.
Usando o mesmo raciocínio, podemos apenas imaginar (sem figura) que vamos agora partir do cubo. Quando ele é deslocado na quarta direção, suas 12 arestas (verdes) criam mais 12 arestas (vermelhas) ao final do percurso. Porém, cada um de seus 8 vértices gera uma nova aresta (roxa) quando se desloca. O resultado é o "cubo" 4D (hipercubo), que tem 32 arestas.
A regra, então, é dobrar o número de arestas de um politopo e somar com o número de seus vértices, para encontrar o número de arestas do politopo do degrau imediatamente superior na escada das dimensões. Mas, nesse estudo, a seqüência dos números de arestas dos politopos ortogonais (1, 4, 12 e 32) não deixa evidente a sua regra de formação. Se você quiser uma fórmula direta, saiba que um politopo ortogonal de n dimensões possui 2n-1n arestas.
O número de faces (quadradas) dos politopos ortogonais pode ser calculado com base em uma regra análoga a essa que vimos para o cálculo do número de arestas. O lado esquerdo da figura 9.3 mostra o "cubo" 2D (quadrado), que tem apenas 1 face (verde). Quando esta se desloca (para cima), vai criar uma nova face (vermelha) ao final do percurso. Porém, cada uma de suas 4 arestas gera uma nova face (roxa) quando se desloca. Desse modo, o cubo (3D) resultante, mostrado com a face frontal aberta, para melhor visualização, fica com 6 faces.
Vamos partir agora do cubo (3D), no lado direito da figura 9.3. Quando ele for deslocado (na quarta direção), cada uma de suas 6 faces (verdes) vai criar uma nova face (vermelha) ao final do percurso. Porém, cada uma de suas 12 arestas vai gerar uma nova face (roxa) quando for deslocada. Assim, conclui-se que o hipercubo (4D) resultante terá um total de 24 faces.
Pode-se ver com isso que dobrando o número de faces de um politopo ortogonal e somando com o seu número de arestas vamos encontrar o número de faces do politopo do degrau imediatamente superior. Se você quiser uma fórmula direta, saiba que um politopo ortogonal de n dimensões possui 2n-3n(n-1) faces quadradas.
Como você já sabe que o hipercubo (4D) é formado por 8 cubos, há um outro modo de calcular o seu número de faces quadradas. Se os cubos que o formam estivessem separados, teríamos um total de 48 faces, porque cada um deles tem 6 faces. Mas, para montar o hipercubo, teremos de colar esses cubos uns nos outros pelas suas faces quadradas. Cada par de faces será colado junto e se transformará em somente 1 face. Portanto, as 48 faces dos cubos separados resultarão em 24 faces no hipercubo, confirmando o resultado a que chegamos antes. Cada face do hipercubo vai pertencer, então, a 2 cubos diferentes (48 / 2 = 24).
De modo semelhante, podemos descobrir outra característica do hipercubo (4D), porque já sabemos que ele tem 32 arestas. Se os 8 cubos que o formam estivessem separados, o total de arestas seria 96, porque cada um deles tem 12. Para que essas 96 arestas possam se transformar em somente 32 no hipercubo, fica claro que cada uma delas deve pertencer a 3 cubos diferentes (96 / 3 = 32).
Da mesma forma, se o hipercubo tem 16 vértices, mas o total de vértices contidos em 8 cubos separados é 64, fica também claro que cada vértice do hipercubo deve pertencer a 4 cubos diferentes (64 / 4 = 16).
Mais um pequeno esforço. Se num segmento cada vértice pertence a 1 aresta, se num quadrado cada vértice pertence a 2 arestas e se num cubo cada vértice pertence a 3 arestas, num hipercubo cada vértice vai pertencer a 4 arestas.
Um pouco mais, ainda. Se num quadrado cada aresta pertence a 1(uma) face e se num cubo cada aresta pertence a 2(duas) faces, num hipercubo cada aresta vai pertencer a 3(três) faces.
Resumindo o que já sabemos e acrescentando um pouco mais, temos que o hipercubo possui 16 vértices, 32 arestas, 24 faces quadradas e 8 células cúbicas. Cada vértice pertence a 4 arestas, a 6 faces e a 4 células. Cada aresta pertence a 3 faces e a 3 células. Cada face pertence a 2 células.
Se você estiver empolgado com o hiperespaço e quiser explorar muitas dimensões mais, há uma fórmula geral:
- se o número de dimensões de um politopo ortogonal for n, e o número de dimensões do elemento geométrico considerado for k, a quantidade desses elementos será dada por C(n,k)2n-k, onde C(n,k) é o número de combinações simples de " n" objetos tomados em grupos de "k".
Como exemplo de uso da fórmula, vamos calcular o número de arestas de um cubo comum. Se o elemento é aresta, que tem 1 dimensão, então k=1. Se o cubo é o politopo ortogonal de 3 dimensões, então n=3. A fórmula fica assim, por substituição dos valores: C(3,1)23-1. O resultado é 12. Portanto, o cubo tem 12 arestas. E quantas células tem um hipercubo? Como as células são cubos comuns, que têm 3 dimensões, k=3. Como o hipercubo considerado tem 4 dimensões, n=4. Substituindo na fórmula ficamos com C(4,3)24-3, cujo resultado é 8. Portanto, o hipercubo (4D) tem 8 células. E o número de faces quadradas do mesmo hipercubo? Como as faces têm 2 dimensões, k=2. Como o hipercubo tem 4 dimensões, n=4. A quantidade de faces será dada por C(4,2)24-2, cujo resultado é 24. Portanto, o hipercubo (4D) tem 24 faces quadradas.
Sem forçar demais, procure agora juntar tudo o que descobrimos sobre o hipercubo. Pense a respeito, com muita atenção. Veja como é possível conhecer as propriedades de um objeto de 4 dimensões, dentro da mais pura lógica, ainda que nunca o possamos ver nem construir fisicamente. Não é incrível que 8 cubos possam ser colados uns nos outros, num espaço 4D, para formar uma estrutura de características geométricas tão interessantes quanto estranhas?
Veja o desespero de Eck, na figura 9.4, ao olhar para 6 quadrados e tentar imaginar um cubo (3D) formado com eles. Sinta você o mesmo, ao olhar para 8 cubos e tentar imaginar um hipercubo (4D). Lembre-se sempre de que tentar enxergar de fato um hipercubo é tão inútil para nós quanto Eck tentar enxergar um cubo. Mas, apesar disso, nem tudo está perdido, porque, do mesmo modo como Eck pode ver a projeção de um cubo sobre seu universo 2D, nós também podemos ver a projeção de um hipercubo sobre nosso espaço 3D.
Há três maneiras de visualizar o Tesseract.
(1) o método da analogia do desdobramento.
(2) o método de olhar a sombra em uma dimensão mais baixa.
(3) o método do corte.
Método 1
Suponha que você tem que fazer um modelo de um cubo 3D, de modo a que um habitante da “Flatland” possa visualizar. Uma maneira de fazer isto pode ser a de desdobrar o cubo e esticá-lo um um plano (como uma dobradura de papel). A criatura 2D agora poderá ao menos observar os lados do objeto e poderá começar a fazer algum senso do que seria o objeto dobrado em sua forma 3D usual.
Como um hipercubo desdobrado apareceria esticado na 3D? Em vez de esticado em áreas, como há no diagrama acima, ele deve ser esticado em volumes. Apenas porque as áreas acima são quadrados 2D, enquanto que os volumes que emergiriam de hipercubo desdobrado devem ser cubos 3D. A representação 3D desdobrada de um hipercubo deve ser algo como o seguinte objeto:
Esta forma da projeção do hipercubo foi feita por Kites como mostrado abaixo:
Também foi mostrado nas artes, como nesta pintura de Salvador Dali:
Método 2
Outra maneira de se mostrar como um cubo 3D seria visto por uma criatura 2D seria iluminando um objeto e observando as sombras projetadas em um plano bidsimensional. A criatura 2D tentaria então ineferir, a partir destas sombras, como o objeto 3D seria visto.
Qual é a situação análoga para o hipercubo? Abaixo se vê a projeção de 8 volumes do hipercubo projetados em perspectiva em 3D
e em rotação:
hipercubo
Método 3
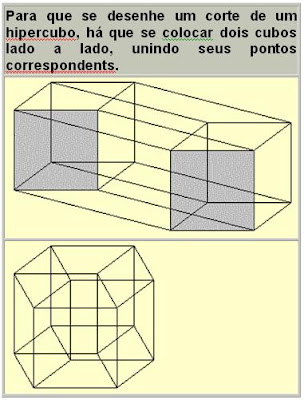
A última maneira de se representar um cubo 3D na 2D é a de cortá-lo, fazendo secções, tal qual se faze em arquitetura ou em estudos anatômicos. Um cubo então é visto como muitos quadrados que fazem uma composição:
Uma “fatia” de um hipercubo sera um cubo 3D. Este corte mostrará então volumes no lugar de areas:
Este modelo de hipercubo foi primeiramente feito por Claude Bragdon em seu livro de 1913 “A Primer of Higher Space.” Bragdon foi o arquiteto que incorporou este e outros “designs” 4D em suas construções. A Câmara de Comércio de Rochester , New York, foi um deles.
Rochester
Aqui uma projeção 3d de um hipercubo em rotação:
Assinar:
Comentários (Atom)