4D - Quarta Dimensão
texto e imagens: Dr. Bernardo de Gregório
revisão, atualização, pesquisas, textos e imagens complementares: Zoia Petrow
Fonte: Grupo de estudos Cinturão de Fótons 2004
Na Europa no fim do Século XIX falar sobre a quarta dimensão era tema restrito a determinados círculos sociais. Eventualmente a idéia da quarta dimensão cruzou o Atlântico e veio aos Estados Unidos. O introdutor principal de todas as idéias quadridimensionais foi um matemático inglês nomeado Charles Hinton. Hinton gastou sua vida obcecado pela noção de popularizar e de visualizar a quarta dimensão. Em 1885, foi preso por bigamia na Inglaterra, por três dias. Logo em seguida, viajou para o Japão, eventualmente terminando nos E. U. em 1893.
Hinton quis criar nomes para as direções e sentidos da quarta dimensão, assim como existem na terceira:
‘para frente” e ‘para trás’
‘esquerda’ e ‘direita’
‘para cima’ e ‘para baixo’
As palavras correspondentes para a quarta dimensão eram “Ana” e “Kata”. Desta forma, se você fosse no sentido do ana na quarta dimensão então você estava indo no sentido oposto de alguém que fosse no sentido do kata.
Hinton foi também a pessoa que pensou o nome para o hipercubo quadridimensional. Chamou-o de “Tesseract”. Este hipercubo é a generalização do cubo tridimensional. Todos seus lados devem ter o mesmo comprimento.
O estudo dos politopos é um ótimo exercício para ampliar nossa visão 4D. Vamos agora utilizar as analogias para prever o número de vértices, arestas,
faces e células do hipercubo (4D) e apresentar algumas fórmulas matemáticas para calcular o número de elementos dos politopos ortogonais, que são os análogos do cubo na escada das dimensões.9.1
A figura 9.1 mostra como é simples encontrar o número de vértices de qualquer politopo ortogonal. Já vimos que o ponto, o segmento (de reta) e o quadrado são os análogos do cubo nos degraus inferiores da escada. Vamos começar com o "cubo" 0D (zero dimensão), que é o ponto. Ele tem somente 1 vértice. Quando ele é deslocado na primeira direção (para a direita), cria o "cubo" 1D (segmento), que tem 2 vértices. Quando o "cubo" 1D é deslocado na segunda direção (para trás), cria o "cubo" 2D (quadrado), que tem 4 vértices. Quando o "cubo" 2D é deslocado na terceira direção (para cima), cria o cubo 3D (o nosso cubo comum), que tem 8 vértices. Assim, seguindo a lógica, quando o cubo for deslocado na quarta direção, ele criará o hipercubo ("cubo" 4D), que é um politopo de 16 vértices.
Você deve ter notado, pela seqüência acima, que nós dobramos o número de vértices a cada degrau que subimos na escada dimensional, porque cada vértice deslocado cria mais um vértice ao final do percurso. Como regra geral, se o número de dimensões de um politopo ortogonal for n, seu número de vértices será 2n.
Vamos agora pensar sobre o número de arestas. No lado esquerdo da figura 9.2, partimos de um "cubo" 1D (segmento), que tem 1 aresta e 2 vértices. Quando ele é deslocado para trás, sua única aresta (verde) cria uma nova aresta (vermelha) ao final do percurso. Porém, cada um de seus 2 vértices gera uma nova aresta (roxa) quando se desloca. O resultado é o "cubo 2D" (quadrado), que tem 4 arestas e 4 vértices.9.2
Vamos partir agora do "cubo" 2D (quadrado), no lado direito da figura 9.2. Quando ele é deslocado para cima, suas 4 arestas (verdes) criam mais 4 arestas (vermelhas) ao final do percurso. Porém, cada um de seus 4 vértices gera uma nova aresta (roxa) quando se desloca. O resultado é o cubo comum (3D), que tem 12 arestas e 8 vértices.
Usando o mesmo raciocínio, podemos apenas imaginar (sem figura) que vamos agora partir do cubo. Quando ele é deslocado na quarta direção, suas 12 arestas (verdes) criam mais 12 arestas (vermelhas) ao final do percurso. Porém, cada um de seus 8 vértices gera uma nova aresta (roxa) quando se desloca. O resultado é o "cubo" 4D (hipercubo), que tem 32 arestas.
A regra, então, é dobrar o número de arestas de um politopo e somar com o número de seus vértices, para encontrar o número de arestas do politopo do degrau imediatamente superior na escada das dimensões. Mas, nesse estudo, a seqüência dos números de arestas dos politopos ortogonais (1, 4, 12 e 32) não deixa evidente a sua regra de formação. Se você quiser uma fórmula direta, saiba que um politopo ortogonal de n dimensões possui 2n-1n arestas.
O número de faces (quadradas) dos politopos ortogonais pode ser calculado com base em uma regra análoga a essa que vimos para o cálculo do número de arestas. O lado esquerdo da figura 9.3 mostra o "cubo" 2D (quadrado), que tem apenas 1 face (verde). Quando esta se desloca (para cima), vai criar uma nova face (vermelha) ao final do percurso. Porém, cada uma de suas 4 arestas gera uma nova face (roxa) quando se desloca. Desse modo, o cubo (3D) resultante, mostrado com a face frontal aberta, para melhor visualização, fica com 6 faces.
Vamos partir agora do cubo (3D), no lado direito da figura 9.3. Quando ele for deslocado (na quarta direção), cada uma de suas 6 faces (verdes) vai criar uma nova face (vermelha) ao final do percurso. Porém, cada uma de suas 12 arestas vai gerar uma nova face (roxa) quando for deslocada. Assim, conclui-se que o hipercubo (4D) resultante terá um total de 24 faces.
Pode-se ver com isso que dobrando o número de faces de um politopo ortogonal e somando com o seu número de arestas vamos encontrar o número de faces do politopo do degrau imediatamente superior. Se você quiser uma fórmula direta, saiba que um politopo ortogonal de n dimensões possui 2n-3n(n-1) faces quadradas.
Como você já sabe que o hipercubo (4D) é formado por 8 cubos, há um outro modo de calcular o seu número de faces quadradas. Se os cubos que o formam estivessem separados, teríamos um total de 48 faces, porque cada um deles tem 6 faces. Mas, para montar o hipercubo, teremos de colar esses cubos uns nos outros pelas suas faces quadradas. Cada par de faces será colado junto e se transformará em somente 1 face. Portanto, as 48 faces dos cubos separados resultarão em 24 faces no hipercubo, confirmando o resultado a que chegamos antes. Cada face do hipercubo vai pertencer, então, a 2 cubos diferentes (48 / 2 = 24).
De modo semelhante, podemos descobrir outra característica do hipercubo (4D), porque já sabemos que ele tem 32 arestas. Se os 8 cubos que o formam estivessem separados, o total de arestas seria 96, porque cada um deles tem 12. Para que essas 96 arestas possam se transformar em somente 32 no hipercubo, fica claro que cada uma delas deve pertencer a 3 cubos diferentes (96 / 3 = 32).
Da mesma forma, se o hipercubo tem 16 vértices, mas o total de vértices contidos em 8 cubos separados é 64, fica também claro que cada vértice do hipercubo deve pertencer a 4 cubos diferentes (64 / 4 = 16).
Mais um pequeno esforço. Se num segmento cada vértice pertence a 1 aresta, se num quadrado cada vértice pertence a 2 arestas e se num cubo cada vértice pertence a 3 arestas, num hipercubo cada vértice vai pertencer a 4 arestas.
Um pouco mais, ainda. Se num quadrado cada aresta pertence a 1(uma) face e se num cubo cada aresta pertence a 2(duas) faces, num hipercubo cada aresta vai pertencer a 3(três) faces.
Resumindo o que já sabemos e acrescentando um pouco mais, temos que o hipercubo possui 16 vértices, 32 arestas, 24 faces quadradas e 8 células cúbicas. Cada vértice pertence a 4 arestas, a 6 faces e a 4 células. Cada aresta pertence a 3 faces e a 3 células. Cada face pertence a 2 células.
Se você estiver empolgado com o hiperespaço e quiser explorar muitas dimensões mais, há uma fórmula geral:
- se o número de dimensões de um politopo ortogonal for n, e o número de dimensões do elemento geométrico considerado for k, a quantidade desses elementos será dada por C(n,k)2n-k, onde C(n,k) é o número de combinações simples de " n" objetos tomados em grupos de "k".
Como exemplo de uso da fórmula, vamos calcular o número de arestas de um cubo comum. Se o elemento é aresta, que tem 1 dimensão, então k=1. Se o cubo é o politopo ortogonal de 3 dimensões, então n=3. A fórmula fica assim, por substituição dos valores: C(3,1)23-1. O resultado é 12. Portanto, o cubo tem 12 arestas. E quantas células tem um hipercubo? Como as células são cubos comuns, que têm 3 dimensões, k=3. Como o hipercubo considerado tem 4 dimensões, n=4. Substituindo na fórmula ficamos com C(4,3)24-3, cujo resultado é 8. Portanto, o hipercubo (4D) tem 8 células. E o número de faces quadradas do mesmo hipercubo? Como as faces têm 2 dimensões, k=2. Como o hipercubo tem 4 dimensões, n=4. A quantidade de faces será dada por C(4,2)24-2, cujo resultado é 24. Portanto, o hipercubo (4D) tem 24 faces quadradas.
Sem forçar demais, procure agora juntar tudo o que descobrimos sobre o hipercubo. Pense a respeito, com muita atenção. Veja como é possível conhecer as propriedades de um objeto de 4 dimensões, dentro da mais pura lógica, ainda que nunca o possamos ver nem construir fisicamente. Não é incrível que 8 cubos possam ser colados uns nos outros, num espaço 4D, para formar uma estrutura de características geométricas tão interessantes quanto estranhas?
Veja o desespero de Eck, na figura 9.4, ao olhar para 6 quadrados e tentar imaginar um cubo (3D) formado com eles. Sinta você o mesmo, ao olhar para 8 cubos e tentar imaginar um hipercubo (4D). Lembre-se sempre de que tentar enxergar de fato um hipercubo é tão inútil para nós quanto Eck tentar enxergar um cubo. Mas, apesar disso, nem tudo está perdido, porque, do mesmo modo como Eck pode ver a projeção de um cubo sobre seu universo 2D, nós também podemos ver a projeção de um hipercubo sobre nosso espaço 3D.
Há três maneiras de visualizar o Tesseract.
(1) o método da analogia do desdobramento.
(2) o método de olhar a sombra em uma dimensão mais baixa.
(3) o método do corte.
Método 1
Suponha que você tem que fazer um modelo de um cubo 3D, de modo a que um habitante da “Flatland” possa visualizar. Uma maneira de fazer isto pode ser a de desdobrar o cubo e esticá-lo um um plano (como uma dobradura de papel). A criatura 2D agora poderá ao menos observar os lados do objeto e poderá começar a fazer algum senso do que seria o objeto dobrado em sua forma 3D usual.
Como um hipercubo desdobrado apareceria esticado na 3D? Em vez de esticado em áreas, como há no diagrama acima, ele deve ser esticado em volumes. Apenas porque as áreas acima são quadrados 2D, enquanto que os volumes que emergiriam de hipercubo desdobrado devem ser cubos 3D. A representação 3D desdobrada de um hipercubo deve ser algo como o seguinte objeto:
Esta forma da projeção do hipercubo foi feita por Kites como mostrado abaixo:
Também foi mostrado nas artes, como nesta pintura de Salvador Dali:
Método 2
Outra maneira de se mostrar como um cubo 3D seria visto por uma criatura 2D seria iluminando um objeto e observando as sombras projetadas em um plano bidsimensional. A criatura 2D tentaria então ineferir, a partir destas sombras, como o objeto 3D seria visto.
Qual é a situação análoga para o hipercubo? Abaixo se vê a projeção de 8 volumes do hipercubo projetados em perspectiva em 3D
e em rotação:
hipercubo
Método 3
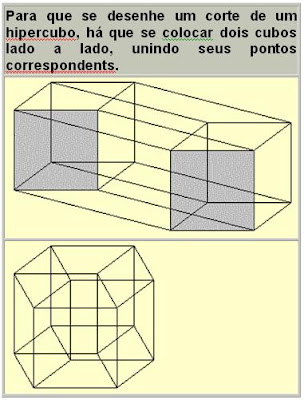
A última maneira de se representar um cubo 3D na 2D é a de cortá-lo, fazendo secções, tal qual se faze em arquitetura ou em estudos anatômicos. Um cubo então é visto como muitos quadrados que fazem uma composição:
Uma “fatia” de um hipercubo sera um cubo 3D. Este corte mostrará então volumes no lugar de areas:
Este modelo de hipercubo foi primeiramente feito por Claude Bragdon em seu livro de 1913 “A Primer of Higher Space.” Bragdon foi o arquiteto que incorporou este e outros “designs” 4D em suas construções. A Câmara de Comércio de Rochester , New York, foi um deles.
Rochester
Aqui uma projeção 3d de um hipercubo em rotação: